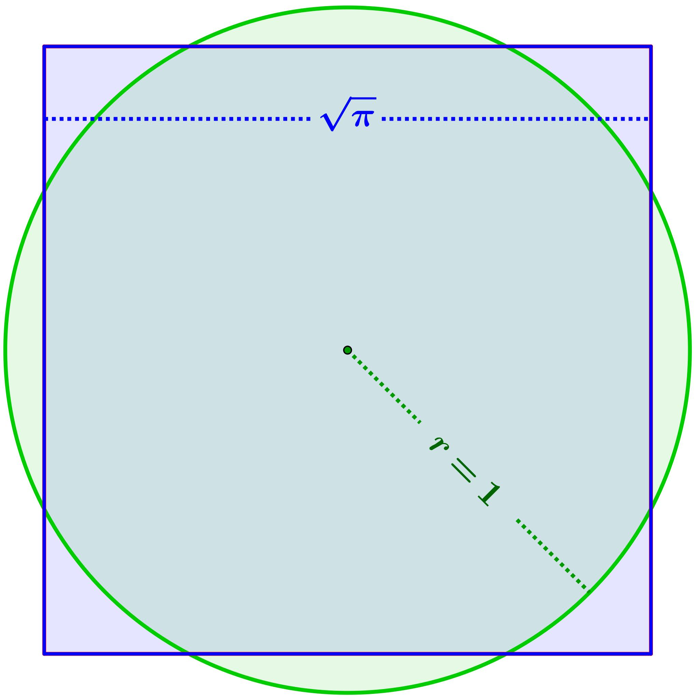
La matematica è una disciplina affascinante per molte ragioni, ma una delle sue caratteristiche più rassicuranti è la sua certezza. Quando qualcosa viene dimostrato, rimane tale per sempre, senza possibilità di ritrattazione secoli dopo. Un esempio emblematico è il pi greco, una costante famosamente irrazionale che non può essere espressa come frazione di numeri interi. Questo fatto è noto da almeno 360 anni, con la prima dimostrazione attribuita a Johann Heinrich Lambert nel 1761.
Tuttavia, nel XIX secolo, il medico e matematico dilettante Edward J Goodwin tentò di dimostrare che il pi greco fosse razionale. Nel 1894, scrisse un articolo affermando questa tesi e successivamente presentò un disegno di legge in Indiana per rendere legale questa sua conclusione. Il Disegno di Legge n. 246 del 1897 proponeva che il valore di pi greco fosse definito come un numero razionale, contrariamente alla realtà matematica consolidata.
Goodwin sosteneva di aver trovato un modo per “raddrizzare il cerchio”, un problema antico che riguarda la possibilità di disegnare un quadrato con la stessa area di un cerchio dato. Tuttavia, raddrizzare il cerchio è un’impresa impossibile, poiché dimostrare tale operazione equivale a dimostrare che il pi greco è razionale, cosa che è stata confutata nel 1882 da Ferdinand von Lindemann.
Il Disegno di Legge sul Pi dell’Indiana proposto da Goodwin non specificava effettivamente il valore di pi greco che si intendeva stabilire come razionale. Le sue argomentazioni erano confuse e contraddittorie, e il disegno di legge fu oggetto di derisione e critiche da parte di esperti matematici.
Clarence Abiathar Waldo, un professore di matematica, intervenne durante la discussione del disegno di legge al Senato dello Stato dell’Indiana e riuscì a scongiurare l’approvazione della proposta. Grazie alla sua competenza e alla sua chiara spiegazione sulla natura irrazionale del pi greco, il disegno di legge fu respinto e archiviato.
Il tentativo di Goodwin di legiferare un valore razionale per il pi greco si rivelò una vicenda assurda e priva di fondamento matematico, che alla fine fu sconfitta dalla razionalità e dalla conoscenza esperta di chi sapeva distinguere la verità dalla fantasia.
Links:
