Il problema del sofà: una soluzione matematica
I matematici di solito non vengono considerati come aiutanti durante un trasloco. E in effetti, perché dovrebbero esserlo? Per decenni, non hanno potuto fornire risposte certe su come far passare un grande divano angolare attraverso un angolo stretto per entrare in un appartamento. Tuttavia, Jineon Baek potrebbe farci cambiare idea su questo aspetto. L’appassionato di combinatoria e geometria dell’Università di Yonsei in Corea ha recentemente pubblicato una dimostrazione di 100 pagine su questo specifico problema, risolvendo così uno dei problemi più urgenti che riguardano il nostro quotidiano, consentendoci di prendere decisioni più informate sull’arredamento prima di rimanere bloccati sulle scale al terzo piano.
Il dilemma del sofà e le sue soluzioni
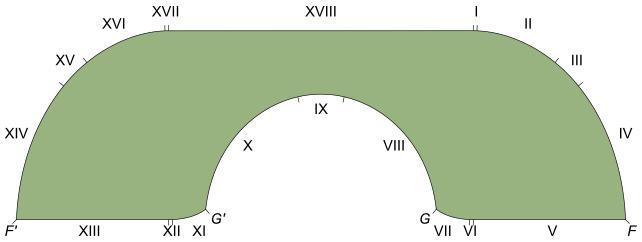
Nel lontano 1966, il matematico austro-canadese Leo Moser formulò un problema che ha afflitto l’umanità da tempi antichi, quando un Australopiteco esausto si trovò intrappolato in una caverna con un comodo cadavere di gazzella che non voleva assolutamente muoversi. A prima vista, sembra un problema semplice: qual è la più grande forma bidimensionale che può passare con successo attorno a un angolo a L? Per un corridoio largo un’unità, una sedia di un’unità quadrata non avrebbe problemi. Al contrario, un rettangolo perfettamente quadrato di due unità si bloccarebbe inevitabilmente. Ma cosa succede se l’oggetto è unico, come un mobile IKEA ispirato a un personaggio de Il Signore degli Anelli e modellato come una vecchia cornetta telefonica?
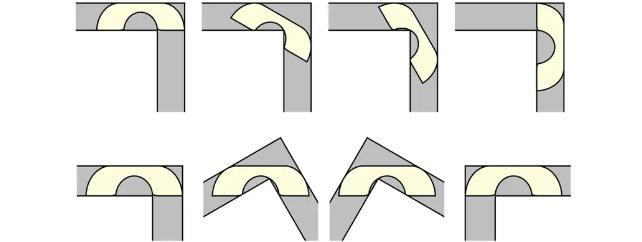
- Appena due anni dopo la formulazione del problema da parte di Moser, il matematico britannico John Hammersley scoprì un sofà composto da un semicerchio sezionato separato da un quadrato con un morso di semicerchio rimosso, che poteva avere un’area di 2,2074 unità e ancora riuscire a passare l’angolo. Per approfondire, puoi leggere questo studio di Hammersley.
- Hammersley stabilì anche un limite superiore per il design, affermando che nulla di più grande di 2,8284 unità sarebbe riuscito a superare l’ostacolo.
- Dopo quasi un quarto di secolo, Joseph Gerver dell’Università di Rutgers suggerì una sottile modifica al sofà di Hammersley, arrotondando alcuni bordi con archi aggiuntivi e trovando una forma che aggiungeva frazioni al limite inferiore precedente, affermando che le dimensioni massime del sofà erano di poco più di 2,2195 unità.
Nonostante le varie soluzioni proposte nel corso degli anni, senza una formula universale che descriva tutte le possibili dimensioni dei mobili, è difficile stabilire con certezza che un sofà leggermente più grande con curve diverse non possa superare l’ostacolo. Nel 2018, i matematici Yoav Kallus dell’Istituto di Santa Fe e Dan Romik dell’Università della California, Davis, utilizzarono un sistema assistito da computer per dimostrare che un sofà potrebbe ragionevolmente essere alto fino a 2,37 unità.
La soluzione definitiva di Baek
Nella sua ultima dimostrazione, Baek ha applicato una magia matematica nota come funzione iniettiva per mappare le forme di successo del sofà di Gerver, fissando proprietà chiave prima di espanderle attraverso dimensioni sempre più grandi per stabilire definitivamente le dimensioni massime di un sofà simile a quello di Gerver. Il risultato? 2,2195 unità è la dimensione massima per un sofà in un corridoio largo un’unità e un angolo a L, confermando la proposta di Gerver del 1992. Anche se la soluzione di Baek deve ancora essere sottoposta a revisione paritaria, potrebbe rappresentare la conclusione definitiva del problema del sofà, almeno in questo contesto.
Prospettive future
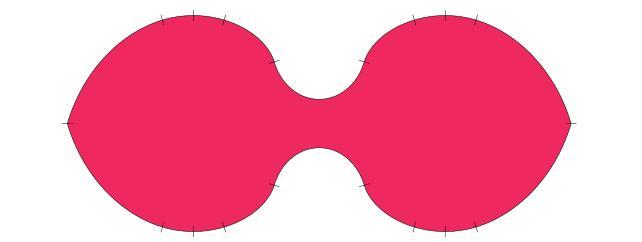
Se hai bisogno di superare un secondo angolo nella direzione opposta, potresti considerare l’acquisto di un sofà ambidestro di Romik, ora disponibile presso IKEA. Questa ricerca è disponibile sul server di pre-pubblicazione arXiv.