La Percezione della Superficie Terrestre
Quando osserviamo l’ambiente che ci circonda, può sembrare che viviamo su una superficie piatta. Questa percezione è comprensibile, poiché è grazie a questa apparente planarità che possiamo orientarci in una nuova città utilizzando una mappa. Tuttavia, oggi sappiamo che abitiamo sulla superficie di una gigantesca sfera, simile a una palla da spiaggia, ma con irregolarità e protuberanze.
Spazi Bidimensionali e Topologia Geometrica
La superficie di una sfera e quella di un piano sono entrambe rappresentazioni di spazi bidimensionali. Possiamo muoverci in due direzioni: nord-sud o est-ovest. Altri spazi bidimensionali includono:
- Superficie di una ciambella
- Superficie di un cilindro
Attraverso la topologia geometrica, i matematici esplorano le varie configurazioni possibili degli spazi in tutte le dimensioni. Questa disciplina è fondamentale in molte applicazioni pratiche, come:
- Progettazione di reti di sensori sicure
- Analisi dei dati
- Uso dell’origami per il lancio di satelliti
La Complessità dello Spazio Tridimensionale
Quando osserviamo l’Universo, percepiamo uno spazio tridimensionale. Tuttavia, se potessimo osservare l’Universo nella sua totalità, scopriremmo che è molto più complesso. I matematici hanno studiato le configurazioni di spazi 2D e 3D, e la nostra comprensione continua a crescere. Questa conoscenza è essenziale per fisici e astronomi che indagano la vera natura dello spazio tridimensionale.
Il Ruolo del Tempo negli Spazi Quadridimensionali
Per descrivere la posizione di un oggetto, come una cometa, sono necessari quattro numeri: tre per le coordinate spaziali e uno per il tempo. Questi valori costituiscono uno spazio quadridimensionale. È interessante riflettere su quali spazi 4D siano possibili e in quale di essi ci troviamo realmente.
Dimensioni Superiori e Applicazioni Pratiche
La teoria delle stringhe suggerisce che l’Universo potrebbe avere molte più dimensioni. Considerare spazi di dimensioni superiori ha applicazioni pratiche, come nella pianificazione del movimento dei robot. Ad esempio, per analizzare il movimento di tre robot su un pavimento, è necessario utilizzare sei coordinate, il che implica uno spazio 6D. Man mano che il numero di robot aumenta, anche la dimensione dello spazio cresce.
Spazi Ad Alta Dimensione nella Scienza
Esistono molte questioni scientifiche in cui si manifestano spazi ad alta dimensione, come:
- Modellazione del movimento di pianeti e veicoli spaziali
- Comprensione della “forma” di grandi set di dati
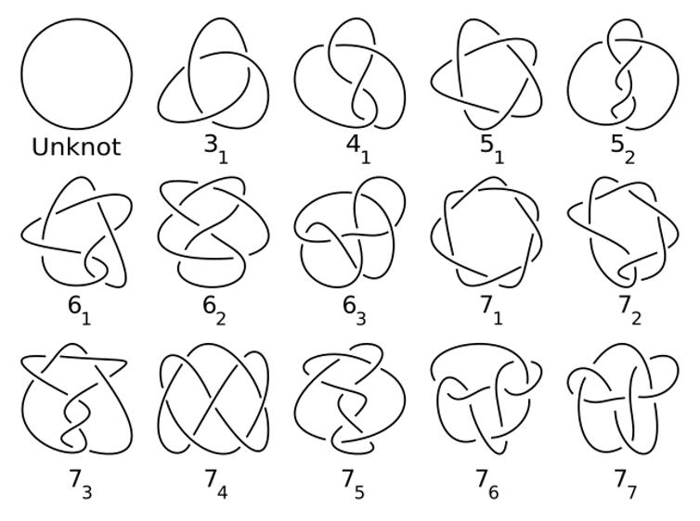
Lo Studio dei Nodi nella Topologia
Un aspetto affascinante della topologia è lo studio di come uno spazio possa trovarsi all’interno di un altro. Ad esempio, un anello di corda annodato rappresenta uno spazio unidimensionale all’interno di uno spazio tridimensionale. L’analisi dei nodi è diventata una branca centrale della topologia, con applicazioni in vari campi, come:
- Teoria delle stringhe in fisica
- Ricombinazione del DNA in biologia
- Chiralità in chimica
La Topologia Geometrica e le Sue Sfide
La topologia geometrica è un campo di studio complesso, ricco di domande stimolanti. La congettura di Poincaré liscia 4D e la congettura del nastro a fette sono solo alcuni esempi delle sfide che attendono risposta. La topologia si rivela utile in numerosi ambiti scientifici e ingegneristici, e scoprire ulteriori misteri riguardanti gli spazi in tutte le dimensioni sarà fondamentale per una comprensione più profonda del mondo in cui viviamo.